从分析力学到电动力学
离散体系
作用量: \[ S=\int L(q,\dot{q},t)\text{d}t \]
动力学方程: \[ \delta S=0\Rightarrow \frac{\text{d}}{\text{d}t}\left(\frac{\partial L}{\partial \dot{q}}\right)-\frac{\partial L}{\partial q}=0 \]
- 此即Euler-Lagrange方程.
连续体系
连续体系的特点:
无穷多自由度. 因此Lagrangian应作为广义坐标的泛函.
离散体系的参数\(i,t\)变为时空坐标\(x^{\mu}\). \[ (x^{\mu})=(ct,\vec{x}) \]
广义坐标: \(\phi=\phi(x^{\mu})\). 被称为场函数.
例子:
- 一维弹性体的广义坐标为\(\xi\), 为\(x\)处弹性体截面移动到的位置.
Lagrangian:
\(L=L[\phi]\), 写开就是 \[ L=\int \mathcal{L}(x^{\mu},\phi,\cdots)\text{d}^3x \]
- 动能项: \(\partial_t \phi\), 势能项为\(\partial_{x,y,z}\phi\), 因此有\(\partial_{\mu}\phi\).
- 不会有更高阶的导数, 否则变分后会出现三阶或更高阶导数, 从而违背基本假设(已知态\((p,q)\)就可预测系统行为).
\[ L=\int \text{d}^3 x\mathcal{L}(x^{\mu},\phi,\partial_{\mu}\phi) \]
- 其中\(\mathcal{L}\)根据其物理含义被称为Lagrangian Density.
作用量 \[ S=\int \text{d}t\int \text{d}^3 x\mathcal {L}=\int\text{d}^4 x\mathcal{L} \]
\(\text{d}^4x\)为四维体积微元, 这时的Lagrangian Density 的会与原来差一个\(1/c\), 如果使用自然单位制就可以忽略这个问题.
四维体积元是Lorentz不变的, 因此如果希望理论是Lorentz协变的, 需要Lagrangian Density 是一个4-scalar.
场方程. \[ \begin{aligned} \delta S &=\int \text{d}\Omega \left(\frac{\partial \mathcal{L}}{\partial \phi}\delta \phi+\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\delta \partial_{\mu}\phi \right)\\ &=\int \text{d}\Omega \partial_{\mu}\left( \delta\phi\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)} \right) -\int\text{d}\Omega \left(\partial_{\mu} \frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi)} - \frac{\partial \mathcal{L}}{\partial \phi}\right) \delta\phi \end{aligned} \]
第一项利用Gauss定理转化为时空边界上的积分, 利用固定边界条件, 这一项为零.
第二项在任意\(\delta\phi\)下恒为零给出场方程: \[ \begin{aligned} \boxed{\partial_{\mu} \frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi)} - \frac{\partial \mathcal{L}}{\partial \phi}=0} \end{aligned} \]
对于矢量场, 其分量分别满足上述方程: \[ \begin{aligned} \boxed{\partial_{\mu} \frac{\partial \mathcal{L}}{\partial (\partial_\mu A^{\nu})} - \frac{\partial \mathcal{L}}{\partial A^{\nu}}=0,\quad \nu = 0,1,2,3} \end{aligned} \]
例子:
自由标量场 \[ \mathcal{L}=\frac{1}{2}(\partial_{\mu}\phi)(\partial^{\mu}\phi) \] 有 \[ 0=\partial_{\mu}\frac{\partial \mathcal{L}}{\partial(\partial_{\mu}\phi)}=\partial_{\mu}\partial^{\mu }\phi \] 此即\(\phi\)的波动方程.
二 源
连续性方程
源的连续性方程: \[ \frac{\partial \rho}{\partial t}+\nabla\cdot\vec{j}=0 \]
引入 \[ (j^{\mu})=(c\rho,\vec{j}) \] 则有 \[ \partial_{\mu}j^{\mu}=0 \]
因为\(0\)是4-scalar, \(\partial_{\mu}\)是4-vector, 因此根据Quotient Rule就可以知道\(j^{\mu}\)是4-vector.
作用量的相互作用项
电磁场的描述\(A^{\mu}\).
如何描述场与源的相互作用. \(\mathcal{L}\)有如下要求:
- 4-scalar
- 线性 (Lorentz力是线性的);
- *规范不变性. \(A^{\mu}\to A^{\mu}+\partial^{\mu}f\) 后作用量不变.
\[ S_{\text{interaction}}=\int -qA_{\mu}\text{d}x^{\mu} \]
带电粒子的协变运动方程. \[ S=\int -mc^2\text{d}\tau-qA_{\mu}\text{d}x^{\mu} \]
自由粒子项: \[ \delta S_{f}=-\int mc\delta \text{d}s=-mc\int\delta \sqrt{ \eta^{\mu\nu}\text{d}x_{\mu }\text{d}x_{\nu}}=-mc\int \eta^{\mu\nu}u^{\nu }\text{d}\delta x^{\mu}\sim \int \frac{\text{d}p_{\mu}}{\text{d}\tau} \delta x^{\mu}\text{d}\tau \]
相互作用项: \[ \delta S_i=\int \delta A_{\mu}\text{d}x^{\mu}+A_{\mu}\text{d}\delta x^{\mu}\sim \int (\partial_{\nu}A_{\mu}-\partial_{\mu}A_{\nu}) u^{\nu}\delta x^{\mu}\text{d}\tau \]
给出 \[ \begin{aligned} \boxed{\frac{\text{d}p_{\mu}}{\text{d}\tau}=qF_{\mu\nu}u^{\nu}}\end{aligned} \]
若定义电磁场: \[ \vec{E}=-\nabla\phi-\frac{\partial \vec{A}}{\partial t},\quad \vec{B}=\nabla\times\vec{A} \] 则协变方程的\(0\)分量给出 \[ \frac{\text{d}E}{\text{d}t}=q\vec{E}\cdot\vec{v} \] \(1\sim 3\)分量给出 \[ \frac{\text{d}\vec{p}}{\text{d}t}=q(\vec{E}+\vec{v}\times\vec{B}) \]
电磁场张量 \[ F_{\mu\nu}:=\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu} \] 为电磁场张量, 是一个反对称张量. 用电场和磁场的分量写出为 \[ (F_{\mu\nu})=\begin{bmatrix} 0 & E_1/c & E_2/c & E_3/c \\-E_1/c &0 & -B_3 &B_2 \\ -E_2/c & B_3 & 0 &-B_1 \\ -E_3/c & -B_2 & B_1 &0 \end{bmatrix} \]
- 有用的性质. \[ F_{\mu\nu}F^{\mu\nu}=\frac{E^2}{c^2}-B^2 \]
源与场的相互作用项. \[ q=\int \text{d}^3 x q \delta (\vec{x}-\vec{x}') \] 则\(S_i\)可以写成 \[ S=-\int\text{d}^3 x q\delta(\vec{x}-\vec{x}') A_{\mu}\frac{\text{d}x^{\mu}}{\text{d}ct}\text{d}ct \] 其中\(q\delta(\vec{x}-\vec{x}')\)本质上是空间上的电荷分布, 而第二项为速度, 合起来就变成4-电流, 此时 \[ \begin{aligned} \boxed{S_i=\int -\frac{1}{c}A_{\mu}j^{\mu}\text{d}\Omega} \end{aligned} \]
三 电磁场
规范与规范对称
电磁场的规范对称性是指系统在如下变换下的不变性 \[ A^{\mu}\to A^{\mu}+\partial^{\mu}f \]
- \(F'_{\mu\nu}=F_{\mu\nu}\)
- \(\delta S'=\delta S\).
规范对称性提供了\(A^{\mu}\)选择上的自由度.
Coulomb规范: \[ \nabla\cdot\vec{A}=0 \]
Lorenz规范: \[ \partial_{\mu}A^{\mu}=0 \]
自由电磁场的Lagrangian Density
几个要求
4-scalar.
关于\(A^{\mu}\)线性(电磁场满足叠加原理).
满足规范对称性.
一个可行的构造是 \[ F_{\mu\nu}F^{\mu\nu} \]
Lagrangian Density \[ \mathcal{L}=-\frac{1}{4\mu_0 c}F_{\mu\nu}F^{\mu\nu} \]
自由电磁场的场方程
具体展开Lagrangian Density: \[ \mathcal{L}=-\frac{1}{2\mu_0c}(\partial_{\alpha}A_{\beta}\partial^{\alpha}A^{\beta}-\partial_{\beta}A_{\alpha}\partial^{\alpha}A^{\beta}) \]
利用: \[ \partial_{\alpha}A_{\beta}=\delta_{\alpha}^{\mu}\eta_{\beta\nu}\partial_{\mu}A^{\nu} \] 有 \[ \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}A^{\nu})}=-\frac{1}{\mu_0 c}(\partial^{\mu}A_{\nu}-\partial_{\nu}A^{\mu})=-\frac{1}{\mu_0 c}{F^{\mu}}_{\nu} \]
Lagrange方程给出 \[ \begin{aligned} \boxed{\partial_{\mu}{F^{\mu}}_{\nu}=0} \end{aligned} \]
- 利用Lorenz规范可以给出 \[ \partial_{\mu}\partial^{\mu}A_{\nu}=0 \] 即\(A^{\mu}\)的所有分量均满足波动方程.
含源的电磁场方程
相比不含源多了 \[ \frac{\partial \mathcal{L}}{\partial A^{\nu}}=-\frac{1}{c}j_{\nu} \] 带回得到 \[ \begin{aligned} \boxed{\partial_{\mu}{F^{\mu}}_{\nu}=\mu_0 j_{\nu}} \end{aligned} \]
Maxwell方程 \[ \nabla\cdot\vec{E}=\rho/\epsilon_0,\quad \nabla\times\vec{B}=\mu_0\vec{j}+\frac{1}{c^2}\frac{\partial \vec{E}}{\partial t} \]
- Maxwell剩下两个方程可以由\(\vec{E},\vec{B}\)的定义给出, 或利用恒等式 \[ \partial_{\alpha}F_{\beta\gamma}+\partial_{\beta}F_{\gamma\alpha}+\partial_{\gamma}F_{\alpha\beta}=0 \]
四 对称性与守恒律
自由电磁场的能动量
诺特定理指出, 在时空平移对称下, 给出能动张量守恒: \[ {\mathcal{T}^{\mu}}_{\nu}=\frac{\partial \mathcal{L}}{\partial (\partial_\mu A^{\alpha})}\partial_{\nu}A^{\alpha}-\mathcal{L}\delta^{\mu}_{\nu} \]
具体计算自由电磁场的能动张量(这里舍去\(1/c\), 因为具有物理意义的Lagrangian Density没有这个系数): \[ \begin{aligned} {\mathcal{T}^{\mu}}_{\nu}=-\frac{1}{\mu_0}{F^{\mu}}_{\alpha}\partial_{\nu }A^{\alpha}-\frac{1}{2\mu_0}\left(\frac{E^2}{c^2}-B^2 \right)\delta^{\mu}_{\nu} \end{aligned} \]
第一项并不对称, 考虑将其对称化: \[ {F^{\mu}}_{\alpha}\partial_{\nu }A^{\alpha}={F^{\mu}}_{\alpha}{F_{\nu}}^{\alpha}+\partial^{\alpha}({F^{\mu}}_{\alpha}A_{\nu})-A_{\nu}\partial^{\alpha}{F^{\mu}}_{\alpha}={F^{\mu}}_{\alpha}{F_{\nu}}^{\alpha}+\partial^{\alpha}({F^{\mu}}_{\alpha}A_{\nu}) \] 因为\(F^{\mu\nu}\)是反对称的, 因此恒有 \[ \partial_{\mu}\partial^{\alpha}({F^{\mu}}_{\alpha}A_{\nu})=0 \] 因此可以将这一项略去而不改变守恒性.
带回得到 \[ \begin{aligned} {\mathcal{T}^{\mu}}_{\nu}=\frac{1}{\mu_0}F^{\mu\alpha}F_{\nu\alpha}-\frac{1}{2\mu_0}\left(\frac{E^2}{c^2}-B^2 \right)\delta^{\mu}_{\nu} \end{aligned} \]
分量
能量守恒 \[ \begin{aligned} \mathcal{T}^{00}&=\frac{1}{\mu_0}F^{0\alpha}F_{0 \alpha}-\frac{1}{2\mu_0}\left(\frac{E^2}{c^2}-B^2 \right)\\ &=\frac{1}{2}\epsilon_0E^2+\frac{1}{2\mu_0}B^2 \quad \text{Energy Density} \end{aligned} \]
\[ \begin{aligned} &\mathcal{T}^{0i}=\frac{1}{\mu_0}F^{0\alpha}F_{i \alpha}=\left(\frac{1}{\mu_0}\vec{E}\times\vec{B} \right)^i\\ &\text{Poynting Vector} \end{aligned} \]
动量守恒 \[ \mathcal{T}^{i0}=(\frac{1}{\mu_0}\frac{1}{c^2}\vec{E}\times\vec{B})^i=\vec{g}^i \quad \text{Momentum Density} \]
动量张量 \[ \mathcal{T}^{ij}=-\epsilon_0E_iE_j-\frac{1}{\mu_0}B_iB_j+\omega_{\text{E.M.}}\delta_{ij} \] 为负的Maxwell应力张量
含源情况
只需要改写Lagrangian Density的项和利用电磁场方程化简的项: \[ {\mathcal{T}^{\mu}}_{\nu}=-\frac{1}{\mu_0}F^{\mu\alpha}F_{\nu\alpha}-\frac{1}{2\mu_0}\left(\frac{E^2}{c^2}-B^2 \right)\delta^{\mu}_{\nu}-j^{\mu}A_{\nu}+j_{\alpha}A^{\alpha}\delta^{\mu}_{\nu} \] 考虑源贡献的两项: \[ \begin{aligned} &\partial_{\mu}(j_{\alpha}A^{\alpha}\delta^{\mu}_{\nu}-j^{\mu}A_{\nu})\\ &=\partial_{\nu}j_{\alpha}A^{\alpha}-j^{\mu}\partial_{\mu}A_{\nu}\\ &=F_{\nu\mu}j^{\mu}+A_{\mu}\partial_{\nu}j^{\mu} \end{aligned} \]
上述结果比我们所期待的多出了一项\(A_{\mu}\partial_{\nu}j^{\mu}\), 原因是含源的电磁场本身由于给定了源的分布而不再具有时空对称性, 系统不再满足能动量守恒. 但我们可以仿照Noether定理推导的过程, 假设一个时空平移变换的过程, 得到新的Lagrangian Density和\(S'\). 虽然此时不再有\(S'=S\), 但是由于Lagrangian的形式没有发生变化, 因此有\(\delta(S'-S)=0\)仍然成立. 具体计算时前部分和Noether定理完全一致, 但考虑到源随时空平移的变化而变化, 在计算Lagrangian Density时会多出一项: \[ \frac{\partial \mathcal{L}}{\partial j^{\mu}}\partial_{\nu}j^{\mu}\Delta x^{\nu} \] 对比发现这一项就是前式中多出的一项. 因此有 \[ \begin{aligned} \boxed{\partial_{\mu}{\mathcal{T}^{\mu}}_{\nu}=-F_{\nu\mu}j^{\mu}} \end{aligned} \]
容易验证分量形式: \[ \frac{\partial \omega_{\text{E.M.}}}{\partial t}+\nabla\cdot\vec{S}=-\vec{E}\cdot\vec{j} \]
\[ \frac{\partial \vec{g}}{\partial t}+\nabla\cdot \mathbf{G}=-\rho\vec{E}-\vec{j}\times\vec{B} \]
规范对称性
系统满足规范对称性 \[ 0=\Delta S=\int \text{d}\Omega \frac{1}{c}(\partial_{\mu} f )j^{\mu},\quad A^{\mu}\to A^{\mu}+\partial^{\mu}f \] 分部积分得到 \[ \boxed{\partial_{\mu}j^{\mu}=0} \] 即电荷守恒.
问题: 事实上, 规范对称性实际上只是一种数学描述的冗余而不含有任何物理含义, 因此严格意义上讲不算一种对称性. 对于这个问题存在一些争论.
A-B effect
Aharonov和Bohm于1959年设计实验说明, 物质波的非局域性导致其只能感受到电磁场的积分结果, 因此用\(A^{\mu}\)的描述更加自然. (仅此而已, 不能说明\(A^{\mu}\)和\(E,B\)哪一个更本质)
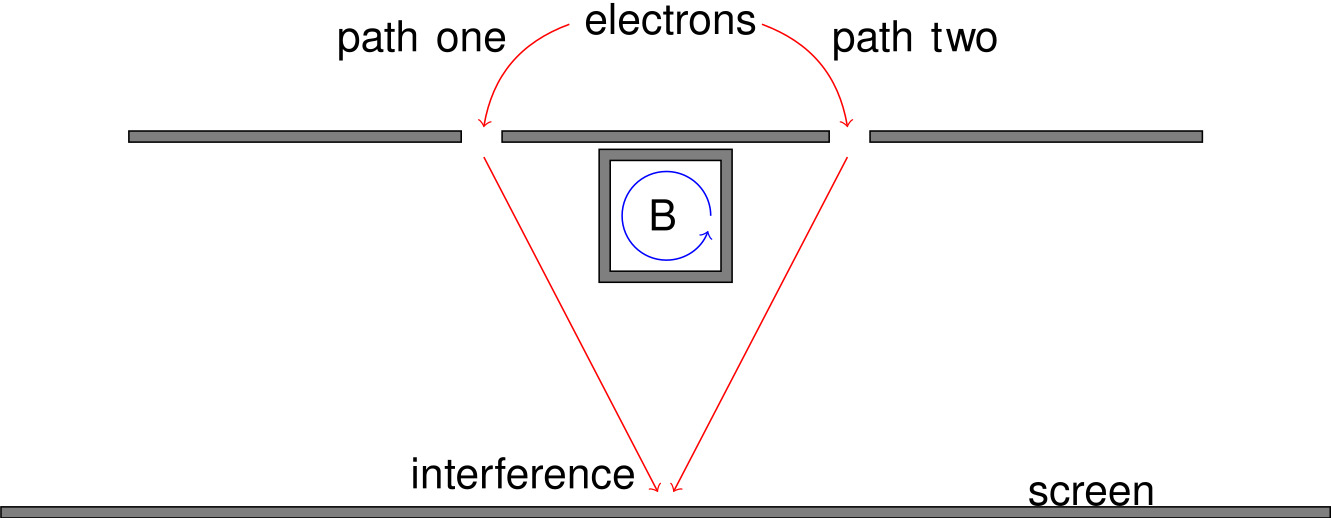
实验具体内容为电子的双缝干涉, 中间加一块磁场, 根据量子力学, 两列电子会产生额外相位差 \[ \Delta \phi=\frac{e}{\hbar}\oint \vec{A}\cdot\text{d}\vec{l} \] 从而使电子双缝干涉图样产生一个平移. 实际上在电子运动范围内不存在磁场. 从而是\(\vec{A}\)影响了电子的行为.
More about Gauge Symmetry
一般的规范对称性是指复标量场在变换下 \[ \phi \to e^{ie\alpha}\phi \] 下不变的性质. 即\(\text{U}(1)\)不变性. 满足这一点的一个Lagrangian Density 为 \[ \mathcal{L}=-\partial_{\mu}\bar{\phi}\partial^{\mu}\phi-u(\phi\bar{\phi}) \] 取\(\alpha\to 0\)的导数就得到对应的守恒流 \[ j^{\mu}=ie(\phi\partial^{\mu}\bar{\phi}-\bar{\phi}\partial^{\mu}\phi) \]
若将相位局域化: \(\alpha\to \alpha(x^{\mu})\), 则变换下\(\Delta S\)会多出 \[ \int \text{d}\Omega j^{\mu}\partial_{\mu}\alpha \] 项. 为此一个好的办法是引入一个矢量场\(A^{\mu}\), 使其在规范变换下满足 \[ A^{\mu}\to A^{\mu}+\partial^{\mu}\alpha \] 并且为Lagrangian Density引入耦合项 \[ j^{\mu}A_{\mu} \] 就可以抵消掉新产生的作用量的变化项.
再考虑\(j^{\mu}\)的变化. 注意到在规范变换下 \[ (\partial_{\mu}-ieA_{\mu})\phi\to e^{ie\alpha}(\partial_{\mu}-ieA_{\mu})\phi \] 因此可以引入新的协变导数算符: \[ D_{\mu}:=\partial_{\mu}-ieA_{\mu} \] 就可以找到的新的守衡流 \[ J^{\mu}=ie(\phi\overline{D_{\mu}\phi}-\bar{\phi}D_{\mu}\phi) \]
上述内容中表明, 全局(global)的规范对称和局域(local)的规范对称是有本质区别的. 一般认为global的规范对称是一种真实的物理对称(对此的物理解释是, 只有电荷守恒, \(A\)在规范变换下体系的能量才不会有区别. 如果电荷不守恒, 凭空产生电荷所需的能量就与所选取的规范有关.), 而局域性的规范对称只是数学上的冗余, 规范场论的描述是因为这样数学上的冗余带来的计算上的方便. 事实上, 在最初的推导中, 我们没有使用Noether定理的结论: 场变换下 \[ \frac{\partial \mathcal{L}}{\partial(\partial_{\mu}A^{\nu})}\delta A^{\nu} \] 守恒. 带入就是 \[ {F^{\mu}}_{\nu}\partial^{\nu}f\sim -f\partial^{\nu}{F^{\mu}}_{\nu}\sim fj^{\mu} \] 若要由此推出电荷守恒, 就要求规范势\(f\)是一个常数, 即global的.